دو ریاضیدان در تاریخ ۷ سپتامبر اثبات خود برای مدلی از مشهورترین مسائل ریاضی را ارائه دادند. نتایج این اثبات، چشمانداز جدیدی به بررسی فرضیهی اعداد اول دوقلو باز کرده است که بیش از یک قرن ذهن ریاضیدانها را به خود مشغول کرده است. این فرضیه راهگشای پیچیدهترین مسائل علم حساب خواهد بود. بهگفتهی جیمز ماینارد، ریاضیدان دانشگاه آکسفورد:
مدتها در حال درجا زدن بودیم و ایدهای برای حل این مسئله نداشتیم بنابراین وقتی ایدههای جدید مطرح شدند ناخودآگاه هیجانزده شدیم.
اعداد اول دوقلو، به زوج اعداد اول با تفاضل ۲ گفته میشود. زوجهای عددی ۵ و ۷ یا ۱۷ و ۱۹ از اعداد اول دوقلو هستند. براساس این فرضیه بینهایت زوج عدد اول دوقلو در میان اعداد صحیح وجود دارد. ریاضیدانها در زمینهی حل این فرضیه در دههی گذشته به شکل چشمگیری پیشرفت کردهاند اما تاکنون قادر به حل آن نشده بودند.
ویل ساوین از دانشگاه کلمبیا و مارک شوسترمان از دانشگاه ویسکانسین مادیسون در اثبات جدید خود، فرضیهی اعداد اول دوقلو را برای محدودهی کوچکتری از اعداد حل کردند. آنها این فرضیه را برای یک مجموعه از دستگاههای عددی متناهی ثابت کردند که ممکن است دربردارندهی مجموعهی محدودی از اعداد اول دوقلو باشد.

به دستگاههای عددی فوق، «میدانهای متناهی» گفته میشود. با اینکه این مجموعه از نظر اندازه کوچک است اما میتوان اغلب ویژگیهای اعداد صحیح نامتناهی را در آن یافت. ریاضیدانها در تلاشاند به سؤالهای ریاضی روی میدانهای متناهی پاسخ دهند و نتایج را به اعداد صحیح هم تعمیم دهند. بهگفتهی ماینارد:
برای رسیدن به رویایی نهایی در ابتدا باید به درک مناسبی از دنیای میدانهای متناهی رسید سپس این نتیجه میتواند راه خود را به دنیای اعداد صحیح باز کند
ساوین و شوسترمان علاوه بر اثبات فرضیهی اعداد اول دوقلو به نتیجهی فراگیرتری دربارهی رفتار اعداد اول در دستگاههای عددی کوچک رسیدهاند. آنها به محاسبهی تعداد تکرار اعداد اول دوقلو روی بازههای کوچکتر پرداختند. از این نتیجه میتوان برای کنترل دقیقتر اعداد دوقلوی اول استفاده کرد. ریاضیدانها امیدوار هستند برای اعداد ترتیبی هم به نتایج مشابهی برسند؛ آنها اثبات جدید را برای اعداد اول روی محور حقیقی بررسی خواهند کرد.
نوع جدیدی از اعداد اول
براساس مشهورترین پیشبینی فرضیهی اعداد اول دوقلو میتوان بینهایت زوج عدد اول با تفاضل ۲ پیدا کرد؛ اما این فرضیه فراتر از صرفا تفاضل ۲ است. برای مثال میتوان بینهایت زوج عدد اول با اختلاف ۴ (مانند ۳ و ۷) یا ۱۴ (۲۹۳ و ۳۰۷) و بهطور کلی تفاضل دلخواه بیشتر از ۲ پیدا کرد.
آلفونس دی پولیگناک ، ریاضیدان فرانسوی، در سال ۱۸۴۹ از این فرضیه به شکل امروزی آن استفاده کرد. ریاضیدانها در طول ۱۶۰ سال پس از آلفونس پیشرفت کمی در اثبات این فرضیه داشتند؛ اما نهایتا در سال ۲۰۱۳ این سد شکسته شد. درهمان سال ییتانگ ژانگ ثابت کرد بینهایت زوج عدد اول با تفاضل حداکثر ۷۰ میلیون وجود دارد. سال بعد از این کشف ریاضیدانهای دیگری از جمله ماینارد و تری تائو شکاف اعداد اول را به شکل چشمگیری کاهش دادند. آخرین اثبات، وجود بینهایت زوج عدد اول با اختلاف حداکثر ۲۴۶ بود.
اما پیشرفت فرضیهی اعداد اول دوقلو متوقف شد. ریاضیدانها برای حل کامل این مسئله به ایدهای کاملا جدید نیاز دارند. دستگاههای عددی متناهی جای خوبی برای جستجوی این اعداد هستند. برای ساخت یک میدان متناهی باید به استخراج یک زیرمجموعهی عددی از اعداد طبیعی پرداخت. برای مثال در این روش پنج عدد انتخاب میشود (میتواند شامل اعداد اول هم باشد) و بهجای نمایش متداول اعداد روی محور حقیقی، روی صفحهی ساعت نمایش داده میشوند.
در مرحلهی بعدی محاسبات روی صفحهی ساعت انجام میشوند. برای مثال ۳+۴ در دستگاه عددی متناهی با پنج عدد چیست؟ از ۴ شروع کنید پس از طی سه فاصله اطراف ساعت به عدد ۲ میرسید. تفریق، ضرب و تقسیم هم عملکرد مشابهی دارند.
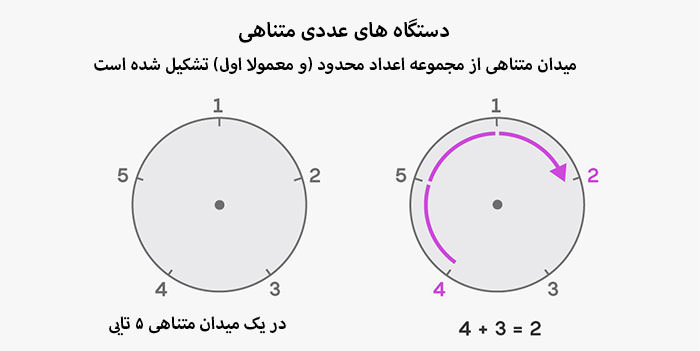
روش میدانهای متناهی تنها یک دستاورد دارد. مفهوم رایج اعداد اول در میدانهای متناهی شکل متفاوتی به خود میگیرد. در یک میدان متناهی هر عدد بر عدد دیگر بخشپذیر است. برای مثال، ۷ معمولا بر ۳ بخشپذیر نیست؛ اما در میدان متناهی با پنج عنصر، چنین رابطهای وجود دارد. به همین دلیل در این میدان متناهی، ۷ مشابه ۱۲ است هر دو در صفحهی ساعت روی ۲ قرار میگیرند؛ بنابراین ۷ تقسیم بر ۳ مشابه ۱۲ تقسیم بر ۳ است؛ و جواب ۱۲ تقسیم بر ۳ برابر با ۴ است.
به همین دلیل، فرضیهی اعداد دوقلوی اول برای میدانهای متناهی دربارهی چندجملهایهای اول مثل x۲+1 صدق میکند. برای مثال، فرض کنید میدان متناهی شما شامل اعداد ۱، ۲ و ۳ است. یک چندجملهای در این میدان متناهی اعدادی را بهعنوان ضریب دربردارد و چندجملهای اول، قابل تجزیه بر چندجملهایهای کوچکتر نیست؛ بنابراین x۲+x +۲ اول است زیرا نمیتوان آن را تجزیه کرد اما x۲-۱ اول نیست زیرا به (x+۱) و (x-۱) قابل تجزیه است.
در چندجملهایهای اول، یافتن چندجملهایهای اول دوقلو هم امری عادی است. چندجملهای اول دوقلو به یک زوج چندجملهای اطلاق میشود که هم اول باشند و هم اختلاف ثابتی با یکدیگر داشته باشند. برای مثال چندجملهای x۲+x +۲ مشابه x۲+۲x+۲ اول است. هر دو دارای اختلاف x هستند (برای رسیدن به چندجملهای دوم، x را به چندجملهای اول اضافه کنید). طبق فرضیهی اعداد اول دوقلو برای میدانهای متناهی، بینهایت زوج چندجملهای اول دوقلو وجود دارد که دارای اختلاف x یا اختلافهای دلخواه دیگر است.
برشهای تمیز
شاید چندجملهایهای اول و میدانهای متناهی به نظر مصنوعی برسند و بهطور کلی کاربرد کمی در علم اعداد داشته باشند اما مشابه یک شبیهساز طوفان عمل میکنند؛ جهانی مستقل که از آن میتوان به دیدگاههایی دربارهی پدیدههای جهان واقعی رسید. بهگفتهی شوسترمان:
براساس یک قیاس کهن بین اعداد صحیح و چندجملهایها، میتوان مسائل مربوط به اعداد صحیح را که معمولا مسائل بسیار دشواری هستند به مسائل چندجملهای تبدیل کرد که دشوار ولی قابل کنترل هستند»
آندره وی در دههی ۱۹۴۰ روشی دقیق برای ترجمهی ریاضیات دستگاههای عددی کوچک به ریاضیات اعداد صحیح ابداع کرد؛ از همین نقطه میدانهای متناهی در مرکز توجه قرار گرفتند. او مهمترین مسئلهی ریاضی یعنی فرضیهی ریمان را برای منحنیهای روی میدانهای متناهی اثبات کرد (مسئلهای که بهعنوان فرضیهی ریمانی هندسی هم شناخته میشود). این اثبات همراهبا یک مجموعه از حدس و گمانهای وی، میدانهای متناهی را بهعنوان چشماندازی غنی برای اکتشافات ریاضی تبدیل کرده است.
براساس دیدگاه کلیدی آندره وی، در میدانهای متناهی میتوان از روشهای هندسی برای پاسخگویی به مسئلههای عددی استفاده کرد. شوسترمان میگوید: «این ویژگی خاص میدانهای متناهی است که میتوان برای حل بسیاری از مسائل به بازتعریف هندسی آنها پرداخت.»
برای درک هندسه در میدانهای متناهی، یک چندجملهای را همارز یک نقطه در فضا درنظر بگیرید. ضرایب چندجملهای هم نقش مختصات مکانی را ایفا میکنند. برای مثال در میدان متناهی ۱، ۲ و ۳، چندجملهای ۲x+۳ در فضای دوبعدی در نقطهی (۲، ۳) قرار میگیرد.
اما حتی سادهترین میدان متناهی هم دارای تعدادی نامتناهی چندجملهای است. میتوان با افزایش اندازهی بزرگترین نما یا درجهی عبارت، چندجملهایهای دقیقتری ساخت. برای مثال چندجملهای x۲-۳x-۱ بهصورت یک نقطه در فضای سهبعدی نمایش داده میشود. چندجملهای ۳x۷+۲x۶+۲x۵-۲x۴-۳x۳+x۲-۲x+۳ بهصورت یک نقطه در فضای هشتبعدی نمایش داده میشود.
فضای هندسی در فرضیهی جدیدشامل کل چندجملهایها با یک درجهی مشخص برای یک میدان متناهی مشخص است. حالا این سؤال مطرح میشود: راهی برای جداسازی کل نقاط نمایشدهندهی چندجملهایهای اول وجود دارد؟ استراتژی ساوین و شوسترمان تقسیم فضا به دو بخش است. یکی از بخشها شامل تمام چندجملهایها با تعداد ضریب زوج و دیگری شامل چندجملهایها با تعداد ضریب فرد است.
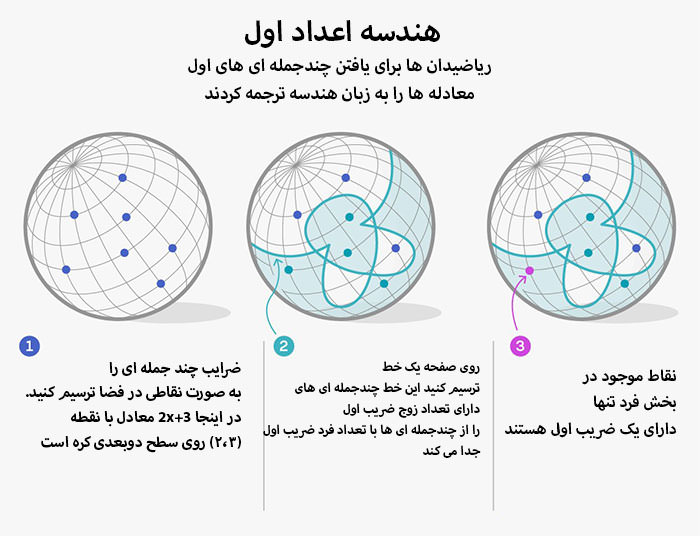
به این ترتیب حل مسئله با تقسیمبندی یادشده آسانتر میشود. فرضیهی اعداد اول دوقلو برای میدانهای متناهی با ضریب یک صدق میکند (همانطور که عدد اول دارای یک ضریب مستقل یعنی خود آن عدد است)؛ و از آنجا که عدد ۱ فرد است میتوان بخشی از فضا با ضریبهای زوج را کاملا نادیده گرفت.
ترفند اصلی حل مسئله در تقسیم است. یک منحنی یکبعدی میتواند فضایی دوبعدی را به دو قسمت تقسیم کند. برای مثال خط استوا سطح زمین را به دو قسمت تقسیم میکند. به همین ترتیب میتوان فضاهای با ابعاد بالاتر را بهوسیلهی سطوحی با ابعاد کمتر تقسیم کرد.
از طرفی شکلهایی با ابعاد کمتر که فضاهای چندجملهای را تقسیم میکنند مانند استوا واضح نیستند. چنین اشیایی براساس فرمولی ریاضی به نام تابع موبیوس ترسیم میشوند که یک چندجملهای را بهعنوان ورودی دریافت میکند و در صورتی که تعداد ضریبهای اول چندجملهای زوج باشد، خروجی ۱، در صورتی که تعداد ضریبهای چندجملهای فرد باشد، منفی ۱ و در صورتی که صرفا دارای یک ضریب تکراری باشد صفر را برمیگرداند (برای مثال ۱۶ را میتوان بهصورت ۲*۲*۲*۲ به دست آورد).
منحنیهایی که توسط تابع موبیوس ترسیم میشوند پیچیده و دارای چرخش زیاد هستند و خود را در بسیاری از نقاط قطع میکنند. تحلیل نقاط تقاطع که تکینگی هم نامیده میشوند کار دشواری است (زیرا متناظر با چندجملهایهایی با ضریب اول تکراری هستند). نوآوری اصلی ساوین و شوسترمان یافتن روشی دقیقی برای برش حلقههایی کم بعد به بخشهای کوتاهتر بود. طبیعتا بررسی بخشهای کوتاهتر آسانتر از بررسی حلقههای کامل است.
ساوین و شوسترمان پس از طبقهبندی چندجملهایها براساس تعداد ضریب اول فرد (سختترین مرحله)، باید مشخص میکردند کدام یک از چندجملهایها اول و کدام یک دوقلوی اول هستند. آنها برای رسیدن به این هدف از فرمولهای متعددی استفاده کردند که معمولا ریاضیدانها برای بررسی اعداد اول در میان اعداد طبیعی به کار میبرند. ساوین و شوسترمان از روش خود برای اثبات دو نتیجهی عمده دربارهی تعداد زیادی از زوج چندجملهایهای اول دوقلو با تفاضل مشخص استفاده کردند.
علاوه بر این اثبات جدید تعداد دقیق چندجملهایهای اول قابل انتظار در میان چندجملهایهایی از یک درجهی مشخص را نمایش میدهد. این دستاورد هم ارز دستیابی به تعداد اعداد اول دوقلو در بازهای طولانی روی محور اعداد حقیقی است؛ نتیجهای رویایی برای ریاضیدانها. زیو رودنیک ریاضیدان میگوید: «این اولین اثباتی است که قیاسی کمی از مقدار قابل انتظار روی بازهای از اعداد صحیح را نمایش میدهد و قبلا چنین نتیجهای به دست نیامده است.»
با وجود گذشت تقریبا ۸۰ سال از اثبات فرضیهی ریمان در منحنیهای میدان متناهی توسط آندره وی، ساوین و شوسترمان نشان دادند که این نظریه امروزه هم کاربرد دارد. امروزه ریاضیدانها پژوهش خود را روی فرضیهی ساوین و شوسترمان متمرکز کردهاند؛ این نظریه میتواند الهامبخش دانشمندان دیگر باشد.
.: Weblog Themes By Pichak :.
